
题目列表(包括答案和解析)
(15分) 如图,已知点P在圆柱OO1的底面⊙O上,AB、A1B1分别为⊙O、⊙O1的直径,且A1A⊥平面PAB.
(1)求证:BP⊥A1P;
 (2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
(2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
(3)在AP上是否存在一点M,使异面直线OM与A1B所成角的余弦值为![]() ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
 在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4| 3 |
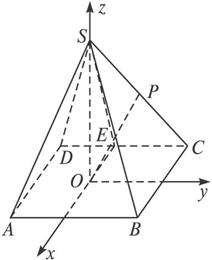
(1)求证:![]() 是定值.
是定值.
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
(文)如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
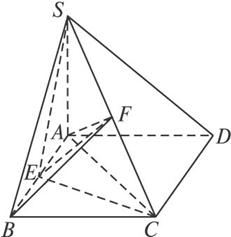
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
完成下列证明![]() ,已知直线a、b、c不共面,它们相交于点P,AÎa,DÎa,BÎb,EÎc
,已知直线a、b、c不共面,它们相交于点P,AÎa,DÎa,BÎb,EÎc
求证:BD和AE是异面直线
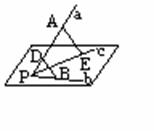
证明:假设__ ![]() 共面于g,则点A、E、B、D都在平面_ _内
共面于g,则点A、E、B、D都在平面_ _内
QAÎa,DÎa,∴__Ìγ. QPÎa,∴PÎ__.
QPÎb,BÎb,PÎc,EÎc ∴_ _Ìg, __Ìg,这与____矛盾
∴BD、AE__________
 ,求直线l的方程;
,求直线l的方程;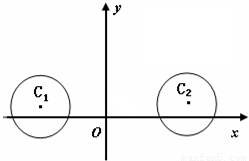
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com