
题目列表(包括答案和解析)
.(本小题满分14分)已知函数f (x)=lnx,g(x)=ex.
( I)若函数φ (x) = f (x)-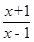 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
. (本小题满分14分)
已知函数 .
.
(I) 若函数 在
在 处取得极值为-1.求
处取得极值为-1.求 、
、 的值;
的值;
(II)若 ,求
,求 的单调区间
的单调区间
(III)在(I)的条件下令 ,常数
,常数 ,若
,若 的图象与
的图象与 轴交于
轴交于 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求证:
,求证:
 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;本小题满分14分)已知正项数列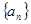 的前
的前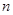 项和为
项和为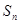 ,且满足
,且满足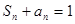 .
.
(I) 求数列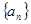 的通项公式;
的通项公式;
(Ⅱ)设数列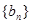 满足
满足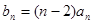 ,且数列
,且数列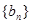 的前
的前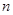 项和为
项和为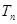 ,
,
求证:数列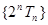 为等差数列.
为等差数列.
(本小题满分14分)
己知.函数![]() 的反函数是
的反函数是![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数都有
,对任意的正整数都有![]() 成立,且
成立,且![]() •
•
(I)求数列![]() 的通项公式; ,
的通项公式; ,
(II)记![]() ,设数列
,设数列![]() 的前n项和为
的前n项和为![]() ,求证:对任意正整数n都有
,求证:对任意正整数n都有![]() ;
;
(III)设数列![]() 的前n项和为
的前n项和为![]() ,已知正实数
,已知正实数![]() 满足:对任意正整数n,
满足:对任意正整数n,![]() 恒成立,求
恒成立,求![]() 的最小值
的最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com