
题目列表(包括答案和解析)
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
数列{an}满足an+1+(-1)n an =2n-1,则{an}的前60项和为
(A)3690 (B)3660 (C)1845 (D)1830
【解析】由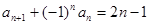 得,
得,
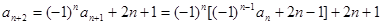
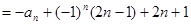 ,
,
即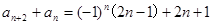 ,也有
,也有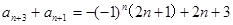 ,两式相加得
,两式相加得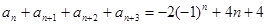 ,设
,设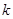 为整数,
为整数,
则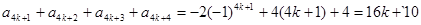 ,
,
于是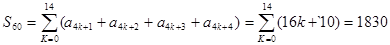
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列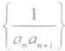 的前100项和为
的前100项和为
(A)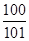 (B)
(B) 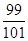 (C)
(C)
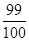 (D)
(D)
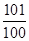
【解析】由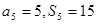 ,得
,得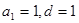 ,所以
,所以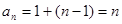 ,所以
,所以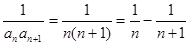 ,又
,又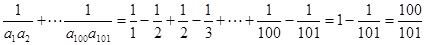 ,选A.
,选A.
 (2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.
(2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.| an | an+1 |
 的最大值.
的最大值.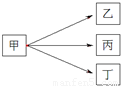
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com