
题目列表(包括答案和解析)
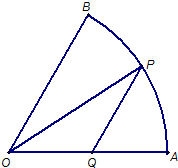 已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.
已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.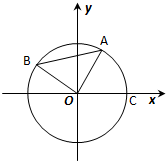 (2012•嘉定区三模)如图,设A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为等边三角形.记以Ox轴正半轴为始边,射线OA为终边的角为θ.
(2012•嘉定区三模)如图,设A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为等边三角形.记以Ox轴正半轴为始边,射线OA为终边的角为θ.| 3 |
| 5 |
| 4 |
| 5 |
| sin2θ+sin2θ |
| cos2θ+cos2θ |
 (2012•嘉定区三模)如图,角θ的始边OA落在x上轴,其始边、终边分别与单位圆交于点A、C(0<θ<
(2012•嘉定区三模)如图,角θ的始边OA落在x上轴,其始边、终边分别与单位圆交于点A、C(0<θ<| π |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
 ,
, ),求
),求 的值;
的值;
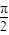 ),△AOB为等边三角形.
),△AOB为等边三角形.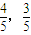 ),求cos∠BOC的值;
),求cos∠BOC的值;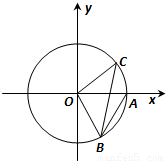
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com