如图1-3-7所示，已知D是△ABC中AB边上一点，DE∥BC且交AC于E，EF∥AB且交BC于F，且S_△ADE =1，S_△EFC=4，则四边形BFED的面积等于(　　)

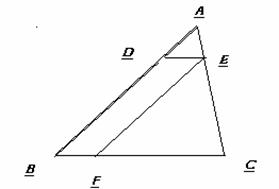
图1-3-7

A.2                       B.4                    C.5                    D.9

如图4-1-7,在直角坐标系中,某车床的两个传动齿轮分别对应圆O₁和圆O₂,其半径分别为1和2,忽略两齿轮的间隙.已知圆O₁上某一点A按顺时针方向旋转的角速度为弧度/秒,当t=0时,⊙O₂上一点B(5,0),当t=14秒时,B运动到B′,则B′的坐标为(    )

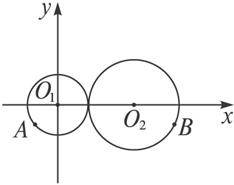
图4-1-7

A.(4,)                      B.(4,)

C.(2,)                      D.(2,)

（本小题满分12分）

    某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图5所示，成绩不小于90分为及格．

甲		乙
257 368 58 68	7 8 9 10	89 678 1235 1

   （Ⅰ）甲班10名同学成绩的标准差      乙班10名同学成绩的标准差（填“>”，“<”）；

   （Ⅱ）从两班10名同学中各抽取一人，已知有人及格，求乙班同学不及格的概率；

   （Ⅲ）从甲班10人中取一人，乙班10人中取两人，三人中及格人数记为X，

图5

求X的分布列和期望．

（本小题满分12分）

    某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图5所示，成绩不小于90分为及格．

甲		乙
257 368 58 68	7 8 9 10	89 678 1235 1

   （Ⅰ）甲班10名同学成绩的标准差      乙班10名同学成绩的标准差（填“>”，“<”）；

   （Ⅱ）从两班10名同学中各抽取一人，已知有人及格，求乙班同学不及格的概率；

   （Ⅲ）从甲班10人中取一人，乙班10人中取两人，三人中及格人数记为X，

图5

求X的分布列和期望．

 [2012·江西卷] 如图1－7，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB＝12，AD＝5，BC＝4，DE＝4，现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合于点G，得到多面体CDEFG.

(1)求证：平面DEG⊥平面CFG；

(2)求多面体CDEFG的体积．

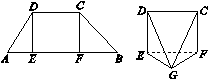
图1－7