(15) 本题主要考查向量共线的充要条件．解:(1)∵=2+8.=3(-) ∴=+=2+8+3(-)=5(+)=5 ∴和共线. 又和有公共点 ∴三点共线 (2)∵——青夏教育精英家教网—

(15) 本题主要考查向量共线的充要条件．解:(1)∵=2+8.=3(-) ∴=+=2+8+3(-)=5(+)=5 ∴和共线. 又和有公共点 ∴三点共线 (2)∵k+与+k共线 ∴存在实数.使k+=(+k) 即(k-)+(1-k)= ∵向量.不共线 ∴ 解得:k=±1 ∴ 当k=±1时.k+与+k共线 (16) 本题主要考查向量的表示以及向量平行和垂直的充要条件的运用．解:=++=(x+4)+(y-2) 又.分别是x.y轴方向上的单位向量 ∴=(6.1).=(x.y).=.= ∵| ∴=0 即 x+2y=0 ① 又 =+=.=+= 且∴·=0 从而得 =0 ② 由①.②解得x=2.y=-1或x=-6.y=3 (17)本题主要考查综合运用正弦定理.余弦定理以及三角形面积公式解三角形和判断三角形形状．解:(1)由题设.易知=60°.且a>b>c ∵= ∴ ac=40 ① 又 a+c=13 ② 由 ①②解得: a=8.c=5 或a=5.c=8 又由余弦定理得: ∴ b=7 ∴ △的三边长为8.7.5. (2)由正弦定理得:2Rsin=a.2Rsin=b. ∴ 2Rsincos=2Rsincos 即 sin2= sin2 由已知.为三角形内角. ∴或 ∴△为直角三角形或等腰三角形. (18)本题主要考查向量的模.向量的数量积的概念.向量平行和垂直的充要条件的运用．解:(1)设=(x.y) ∵ ||=2 ∴ 即 ① 又∵ | .=(1.2) ∴2x-y=0 ② 由 ①②得:x=2.y=4 或 x=-2.y=-4 ∴ =(2.4)或 = (2)∵ (+2)( 2-) ∴(+2)·( 2-)=0 即 3·-2||²=0 ∴ ·=- 又||=.||= ∴ cos==-1 ∵ ∴ = 设点坐标为(x.y).分所成的比为.则 x= . y= =( -2.+1) .= ∵ ∴·=0 ∴ -6(-2)-3(+1)=0 解得 = ∴ x=1 .y=1 故点坐标为(1.1).= 另解:设点坐标为(x.y).AD是BC边上的高. ∴ .与共线又∵=(x = = ∴ 解得:x=1 .y=1 故点坐标为(1.1).= (2)== 由(1)知分所成的比为=. ∴ = ∴ = ∴分所成的比为3 由定比分点坐标公式得:点坐标为(.-1) (20) 解:由三角形面积公式得m= .n= (1) 若...四点共圆.则 ∴= ∴ ²+²==sin² 由余弦定理.在△中. 在△中. ∴= ∵cos=-cos ∴cos= cos²=1- ∴²+²=sin²=1- cos²= (2)²+²= 由余弦定理得: ∴ ∴²+²== = 由条件可知0<<90°(当90°时.矛盾) ∴ <cos<1 从而<²+²< 【查看更多】

题目列表(包括答案和解析)

某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售。如果当天卖不完，剩下的玫瑰花做垃圾处理。

（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n（单位：枝，n∈N）的函数解析式。

（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

日需求量n	14	15	16	17	18	19	20
频数	10	20	16	16	15	13	10

(i)假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；

(ii)若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率.

【命题意图】本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率，是简单题.

【解析】（Ⅰ）当日需求量时，利润=85；

当日需求量时，利润，

∴关于的解析式为；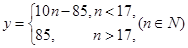

（Ⅱ）(i)这100天中有10天的日利润为55元，20天的日利润为65元，16天的日利润为75元，54天的日利润为85元，所以这100天的平均利润为

=76.4；

(ii)利润不低于75元当且仅当日需求不少于16枝，故当天的利润不少于75元的概率为

查看答案和解析>>

（2012•茂名二模）对人们的休闲方式的一次调查中，共调查了100人，其中女性60人，男性40人．女性中有38人主要的休闲方式是看电视，另外22人主要的休闲方式是运动；男性中有15人主要的休闲方式是看电视，另外25人主要的休闲方式是运动．
（1）根据以上数据建立一个2×2列联表；
（2）判断性别与休闲方式是否有关．参考公式：K²=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

；n=a+b+c+d

p（K²＞k）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.84	5.024	6.635	7.879	10.83

参考数据：60×40×53×47=5978400，620×620=384400，384400÷59784≈6.4298．

查看答案和解析>>

（2012•江苏一模）本题主要考查抛物线的标准方程、简单的几何性质等基础知识，考查运算求解、推理论证的能力．
如图，在平面直角坐标系xOy，抛物线的顶点在原点，焦点为F（1，0）．过抛物线在x轴上方的不同两点A、B，作抛物线的切线AC、BD，与x轴分别交于C、D两点，且AC与BD交于点M，直线AD与直线BC交于点N．
（1）求抛物线的标准方程；
（2）求证：MN⊥x轴；
（3）若直线MN与x轴的交点恰为F（1，0），求证：直线AB过定点．

查看答案和解析>>

经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(km/h)之间的函数关系为y=(v>0).