
题目列表(包括答案和解析)
| 1 |
| z |
| 1 |
| z |
| 3 |
| 2 |
| 1 |
| 2 |
| 6 |
| A、A=30°,B=45° | ||
B、c=1,cosC=
| ||
| C、B=60°,c=3 | ||
| D、C=75°,A=45° |
(本小题满分13分)
古汉集团生产的A,B两种型号的口服液供出口,国家为鼓励产品出口,采用出口退税政策:出口价值为a万元的/1产品可获得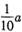 万元的退税款,出口价值为b万元的B产品可获得
万元的退税款,出口价值为b万元的B产品可获得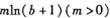 万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
(1) 当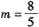 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据:
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据: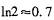 )
)
(2) 记该企业获得的退税款的最大值函数为,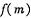 ,求
,求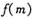 的表达式.
的表达式.
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知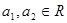 且
且 ,求证
,求证
证明:构造函数 因为对一切
因为对一切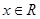 ,恒有
,恒有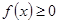 ,所以
,所以 4-8
4-8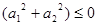 ,从而
,从而
(1)若 ,且
,且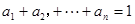 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若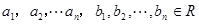 ,求证
,求证
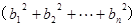
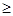
 .[
.[
请阅读下列不等式的证法:已知![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
则![]()
![]()
因为对一切![]() ,恒有
,恒有![]() ≥0,所以
≥0,所以![]() ≤0,从而得
≤0,从而得![]() .
.
请回答下面的问题:
(1)若![]() ,请写出上述结论的推广式
,请写出上述结论的推广式
(2)参考上述证法,请证明你的推广式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com