
题目列表(包括答案和解析)
| 3 |
. |
| z |
复数间的关系
(1)复数相等
①用代数形式描述:
z1=a+bi,z2=c+di(a、b、c、d∈R),
则z1=z2![]() ________.
________.
特殊的,a+bi=0![]() ________.
________.
两个复数不都是实数时,________比较大小.
②用几何形式描述:
z1、z2∈C,z1=z2![]() 对应点Z1、Z2________
对应点Z1、Z2________![]()
![]() 与
与![]() ________.
________.
(2)共轭复数
①定义:若两个复数实部________,虚部________时,这两个复数叫做互为共轭复数,用________表示.
②代数形式:a+bi与________互为共轭复数(a、b∈R),即z=a+bi![]()
![]() =________.
=________.
③几何描述:非零复数z1、z2互为共轭复数![]() 它们的对应点Z1、Z2(或对应向量
它们的对应点Z1、Z2(或对应向量![]() 、
、![]() )关于________对称.
)关于________对称.
④运算性质:
![]() =________;
=________;
![]() =________;
=________;
![]() =________(z2≠0).
=________(z2≠0).
特例:z+![]() =________;z-
=________;z-![]() =________;z·
=________;z·![]() =________;
=________;
z=![]() 是z∈R的________条件;
是z∈R的________条件;
z+![]() =0,且z≠0是z为纯虚数的________条件.
=0,且z≠0是z为纯虚数的________条件.
复数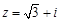 与它的共轭复数
与它的共轭复数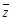 对应的两个向量的夹角为 .
对应的两个向量的夹角为 .
复数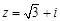 与它的共轭复数
与它的共轭复数 对应的两个向量的夹角为 .
对应的两个向量的夹角为 .
下列命题:
①复平面上向量的集合与复数的集合是一一对应的;
②互为共轭的两个非零复数,它们对应的向量关于实轴对称;
③虚数的共轭复数一定是虚数;
④两个复数互为共轭的充要条件是它们虚部的和为零.其中正确命题的个数是
[ ]
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com