
题目列表(包括答案和解析)
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 (yi-
(yi- i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算 ;
;
(3)比较(1)和(2)中的残差平方和 的大小.
的大小.
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
| 年销售额(千元) | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
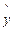 =78+4.2x,计算
=78+4.2x,计算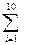 (yi-
(yi-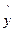 i)2;
i)2; 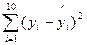 ;
;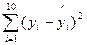 的大小.
的大小.(本小题满分12分)
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?共有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?

(本小题满分12分)
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?共有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?

(本小题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率较高?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com