
题目列表(包括答案和解析)
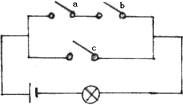
在如图所示的电路中,开关b,a,c开或关的概率都为![]() ,且相互独立,求灯亮的概率.
,且相互独立,求灯亮的概率.
在如图所示的电路图中,“开关A的闭合”是“灯泡B亮”的

A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
 如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有( )
如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有( )
 如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有
如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com