
题目列表(包括答案和解析)
求分别满足下列条件的直线l的方程:
(1)斜率是![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0),B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
[分析]欲求直线的方程,关键是根据已知条件选择一种最合适的形式.
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点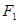 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
若直线l满足如下条件,分别求出其方程.
(1)斜率为![]() ,且与两坐标轴围成的三角形面积为6;
,且与两坐标轴围成的三角形面积为6;
(2)经过两点A(1,0)及B(m,1);
(3)将直线l绕其上一点P沿顺时针方向旋转角α(0°<α<90°)所得直线方程是x-y-2=0,若继续旋转90°-α,所得直线方程为x+2y+1=0;
(4)过点(-a,0),(a>0)且割第二象限得一面积为S的三角形区域.
在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是![]() (-x,-y)
(-x,-y)
(2)关于x轴的对称点是![]() (x,-y)
(x,-y)
(3)关于y轴的对称点是P?(-x,y)
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1________;
(2)关于横轴(x轴)的对称点是P2________;
(3)关于纵轴(y轴)的对称点是P3________;
(4)关于竖轴(z轴)的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点P6________;
(7)关于zOx坐标平面的对称点是P7________.
指出下列各组对象是否能组成集合,若能组成集合则指出集合是有限集,还是无限集,还是空集.
(1)平方等于1的数;
(2)所有的矩形;
(3)著名的数学家;
(4)非常接近于10的数;
(5)平面直角坐标系中,第四象限的点;
(6)被5除余数是2的正数;
(7)平方后等于-1的实数;
(8)15的正约数.
判断一个集合是有限集、空集还是无限集的关键是看集合中元素的个数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com