
题目列表(包括答案和解析)
平面内有两个定点A(-1,0),B(1,0),在圆(x-3)2+(y-4)2=4上求一点P的坐标,使|AP|2+|BP|2达到最大和最小值,并求出最大值和最小值.
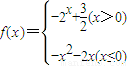 ,则f(x)的“和谐点对”有( )
,则f(x)的“和谐点对”有( )设
A是直角坐标平面上的所有点组成的集合,如果由A到A的映射f,使像集合的元素(y-1,x+2)和原像集合的元素(x,y)对应,那么,像点(3,-4)的原像是点[
]|
A .(-5,5) |
B .(4,-6) |
|
C .(2,-2) |
D .(-6,4) |
设A是直角坐标平面上的所有点组成的集合,如果由A到A的映射f,使像集合的元素(y-1,x+2)和原像集合的元素(x,y)对应,那么,像点(3,-4)的原像是点
[ ]
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系.在平面斜坐标系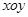 中,若
中,若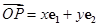 (其中
(其中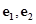 分别是斜坐标系中的
分别是斜坐标系中的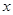 轴和
轴和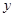 轴正方向上的单位向量,
轴正方向上的单位向量,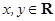 ,
,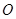 为坐标原点),则称有序数对
为坐标原点),则称有序数对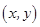 为点
为点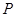 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系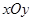 中,若点
中,若点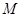 的斜坐标为(1,2),点
的斜坐标为(1,2),点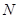 的斜坐标为(3,4),且
的斜坐标为(3,4),且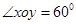 ,则
,则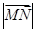 等于 ( )
等于 ( )
A.1
B.2
C.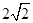 D.
D. 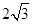
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com