
题目列表(包括答案和解析)
(本题满分14分) 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值.
(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2) 若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换 :
: 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线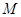 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线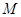 在变换
在变换 下的不动点.
下的不动点.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程. 并求出当
的标准方程. 并求出当 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2)当 时,求(1)中的椭圆
时,求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
 :
: (
( ,
, )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式![]() :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点![]() 变换到这一平面上的一点
变换到这一平面上的一点![]() .
.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2) 若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换![]() 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com