
题目列表(包括答案和解析)
| 为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥。下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg) | ||||||||||||||||||||||
表1:施用新化肥小麦产量频数分布表
表2:不施用新化肥小麦产量频数分布表 | ||||||||||||||||||||||
| (1)完成下面频率分布直方图; | ||||||||||||||||||||||
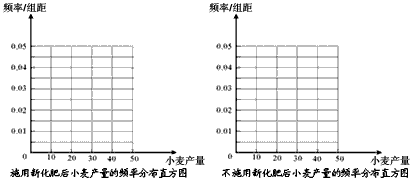 | ||||||||||||||||||||||
| (2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量; (3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异。 | ||||||||||||||||||||||
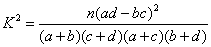
|
设函数![]() 的定义域为D,如果存在正实数k,使对任意
的定义域为D,如果存在正实数k,使对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 在D上的“k阶增函数”。已知
在D上的“k阶增函数”。已知![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() ,其中a为正常数,若
,其中a为正常数,若![]() 为R上的“2阶增函数”,则实数a的取值范围是 ( )
为R上的“2阶增函数”,则实数a的取值范围是 ( )
A.(0,2) B.(0,1) C.![]() D.
D.![]()
集合 ,
, 。若
。若 ,则
,则 的值为:
的值为:
A.0 B.1 C.2 D.4
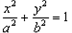 (a>b>0)的离心率为
(a>b>0)的离心率为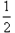 ,且经过点P(1,
,且经过点P(1,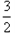 )。
)。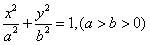 ,其相应于焦点F(2,0)的准线方程为x=4。
,其相应于焦点F(2,0)的准线方程为x=4。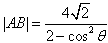 ;
;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com