
题目列表(包括答案和解析)
(本题满分12分)
已知数列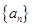 的前
的前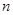 和为
和为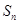 ,其中
,其中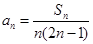 且
且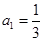
(1)求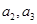
(2)猜想数列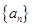 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
(本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
|
|
文艺节目 |
新闻节目 |
总计 |
|
20至40岁 |
40 |
10 |
50 |
|
大于40岁 |
20 |
30 |
50 |
|
总计 |
60 |
40 |
100 |
(1)由表中数据检验,有没有99.9%把握认为收看文艺节目的观众与年龄有关?
(2)20至40岁,大于40岁中各抽取1名观众,求两人恰好都收看文艺节目的概率.

|
P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
(本题满分12分)
已知锐角△ABC中,角A、B、C的对边分别为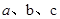 ,
,
且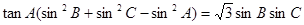 .
.
(1)求角A;
(2)求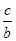 的范围.
的范围.
.(本题满分12分)如图,三棱柱ABC—A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(1)求证:AB1// 面BDC1;
(2)求二面角C1—BD—C的余弦值;
(3)在侧棱AA1上是否存在点P,使得
CP⊥面BDC1?并证明你的结论.

.(本题满分12分)某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果
如下表所示:
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数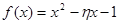 在区间
在区间 ,
,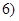 上有且只有一个零点”为事件
上有且只有一个零点”为事件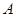 ,求事件
,求事件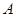 发生的概率
发生的概率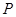 ;
;
(2)从该单位任选两名职工,用 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com