
题目列表(包括答案和解析)
已知在等比数列![]() 中,各项均为正数,且
中,各项均为正数,且![]() 则数列
则数列![]() 的通项公式是
的通项公式是![]() 。
。
已知在等比数列![]() 中,各项均为正数,且
中,各项均为正数,且![]() 则数列
则数列![]() 的通项公式是
的通项公式是![]() 。
。
已知在等比数列 中,各项均为正数,且
中,各项均为正数,且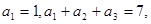 则数列
则数列 的通项公式是
的通项公式是 。
。
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列,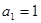 ,且
,且 、
、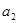 、
、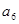 成等比数列。
成等比数列。
⑴求数列 的通项公式;
的通项公式;
⑵设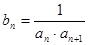 ,求数列
,求数列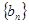 的前
的前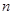 项和
项和 。
。
【解析】第一问中利用等差数列 的首项为
的首项为 ,公差为d,则依题意有:
,公差为d,则依题意有:
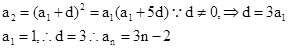
第二问中,利用第一问的结论得到数列的通项公式,
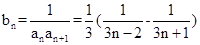 ,利用裂项求和的思想解决即可。
,利用裂项求和的思想解决即可。
(本题满分13分)
已知数列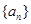 满足
满足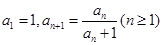 ,数列
,数列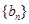 满足
满足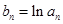 ,数列
,数列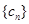 满足
满足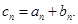
(1)求数列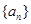 的通项公式;
的通项公式;
(2)试比较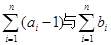 的大小,并说明理由;
的大小,并说明理由;
(3)我们知道数列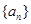 如果是等差数列,则公差
如果是等差数列,则公差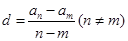 是否会小于等于一个常数k呢?若会,求出k的取值范围;若不会,请说明理由。
是否会小于等于一个常数k呢?若会,求出k的取值范围;若不会,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com