
题目列表(包括答案和解析)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.

【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 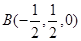 ,P(0,0,2).
,P(0,0,2).

(1)证明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 设平面PCD的法向量
设平面PCD的法向量 ,
,
则 ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
.
所以二面角A-PC-D的正弦值为 .
.
(3)设点E的坐标为(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)证明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如图,作 于点H,连接DH.由
于点H,连接DH.由 ,
, ,可得
,可得 .
.
因此 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值为
的正弦值为 .
.
(3)如图,因为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.| 5 |
|
|
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O是 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。

(I)求证:CD2=DE·DB。
(II)若 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。
(本小题满分10分)
选修4—4:作标系与参数方程
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线 与曲线C交于A,B两点。
与曲线C交于A,B两点。
(I)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(II)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值。
(本小题满分10分)选修4—5:不等式选讲
设函数

(I)画出函数 的图象;
的图象;
(II)若对任意 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O是 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。

(I)求证:CD2=DE·DB。
(II)若 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。
(本小题满分10分)
选修4—4:作标系与参数方程
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线 与曲线C交于A,B两点。
与曲线C交于A,B两点。
(I)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(II)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值。
(本小题满分10分)选修4—5:不等式选讲
设函数

(I)画出函数 的图象;
的图象;
(II)若对任意 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。
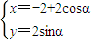 (α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
(α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .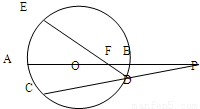
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com