（本题满分8分）将一枚质地均匀的骰子连掷两次，记向上的点数分别为．

（Ⅰ）求事件“”的概率；

（Ⅱ）求事件“方程有实根”的概率．

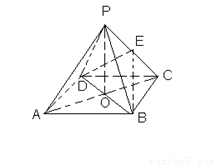
（本题8分）如图，ABCD是正方形，O是正方形的中心， PO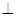底面ABCD，E是PC的中点。

求证：（1）PA∥平面BDE   （2）平面PAC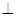平面BDE

（本题8分）某果园要用三辆汽车将一批水果从所在城市E运至销售城市F，已知从城市E到城市F有两条公路。统计表明：汽车走公路Ⅰ堵车的概率为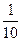，走公路Ⅱ堵车的概率为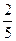，若甲、乙两辆汽车走公路Ⅰ，第三辆汽车丙由于其他原因走公路Ⅱ运送水果，且三辆汽车是否堵车相互之间没有影响。
（Ⅰ）求甲、乙两辆汽车中恰有一辆堵车的概率。
（Ⅱ）求三辆汽车中至少有两辆堵车的概率。

（理）（本题8分）甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中，甲胜乙的概率为，甲胜丙的概率为，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束.

   （1）求只进行两局比赛，甲就取得胜利的概率；  

（2）求只进行两局比赛，比赛就结束的概率；

   （3）求甲取得比赛胜利的概率.

20、（文）（本小题8分）甲、乙两人做定点投篮，投篮者若投中则继续投篮，否则由对方投篮，第一次甲投篮，已知甲、乙每次投篮命中的概率分别为、，且甲、乙投篮是否命中互不影响.

（1）求第三次由乙投篮的概率；

（2）求前4次投篮中各投两次的概率.