
题目列表(包括答案和解析)
设f(x)=x2-x+B,实数a满足|x-a|<1,求证:|f(x)-f(a)|<2(|a|+1).
已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+a x.
x2+a x.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于或等于10.
已知实数a满足1<a≤2,设函数f (x)=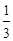 x3-
x3-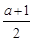 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
已知实数a满足0<a≤2,a≠1,设函数f (x)= x3-
x3- x2+ax.
x2+ax.
(Ⅰ)当a=2时,求f (x)的极小值;
(Ⅱ)若函数g(x)=x3+bx2-(2b+4)x+ln x (b∈R)的极小值点与f (x)的极小值点相同.求证:g(x)的极大值小于等于 .
.
已知实数a满足1<a≤2,设函数f (x)=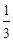 x3-
x3-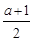 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com