（本小题满分13分）对于在区间[m，n]上有意义的两个函数与，如果对任意[m，n]均有，称与在[m，n]上是接近的，否则称与在[m，n]上是非接近的，现有两个函数与（a＞0，a≠1），给定区间[a＋2，a＋3]．（1）若与在给定区间[a＋2，a＋3]上都有意义，求a的取值范围；（2）讨论与在[a＋2，a＋3]上是否是接近的．

（本小题满分13分）

已知函数是定义在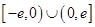上的奇函数,当时,

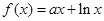(其中e是自然对数的底, )     

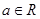   （1）求的解析式;

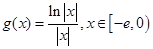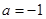   （2）设，求证：当时，；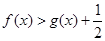

  （3）是否存在实数a，使得当时，的最小值是3 ？如果存在，求出实数a的值；如果不存在，请说明理由。

（本小题满分13分）
在数列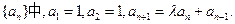
（I）若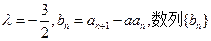是公比为β的等比数列，求α和β的值。
（II）若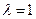，基于事实：如果d是a和b的公约数，那么d一定是a-b的约数。研讨是否存在正整数k和n，使得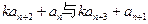有大于1的公约数，如果存在求出k和n，如果不存在请说明理由。

（本小题满分13分）

    设

   （1）如果处取得最小值-5，求的解析式；

   （2）如果的单调递减区间的长度是正整数，试求m和n的值；（注；区间（a，b）的长度为b-a）

（本题满分13分）

检测部门决定对某市学校教室的空气质量进行检测，空气质量分为A、B、C三级．

每间教室的检测方式如下：分别在同一天的上、下午各进行一次检测，若两次检测中有C级或两次都是B级，则该教室的空气质量不合格．   设各教室的空气质量相互独立，且每次检测的结果也相互独立．     根据多次抽检结果，一间教室一次检测空气质量为A、B、C三级的频率依次为，，.

(1) 在该市的教室中任取一间，估计该间教室空气质量合格的概率；

(2) 如果对该市某中学的4间教室进行检测，记在上午检测空气质量为A级的教室间数为X，并以空气质量为A级的频率作为空气质量为A级的概率，求X的分布列及期望值．