练习册

  • 练习册
  • 试题
    某中学三个年级各有十个编号从1到10的班级.为探索教书育人新方法.在全校学生中实施以“立志.立法.立德 为内容的“三立 教育工程.为此在三个年级中抽取14名学生组成第一期“三立 教育指导培训班.要求每个班级至多有一名学生参加.抽取方法是:高一任意抽取8名学生,高二按班级序号的奇偶性分两组各抽取二名,高三抽取2名学生且所抽的班级序号不得相邻.则培训班共有多少种不同的组成方案? 若指派五名教师到三个年级指导“三立 工程实施.要求每个年级至少一人.则有多少种不同的分配方案? 【查看更多】

     

    题目列表(包括答案和解析)

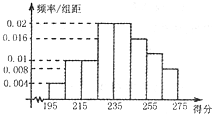
    （2013•郑州一模）某高校组织自主招生考试，共有2000名优秀学生参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成八组：第一组[195，205），第二组[205，215），…，第八组[265，275]．如图是按上述分组方法得到的频率分布直方图，且笔试成绩在260分（含260分）以上的同学进入面试．
    （I）估计所有参加笔试的2000名学生中，参加 面试的学生人数；
    （II）面试时，每位考生抽取三个问题，若三个问 题全答错，则不能取得该校的自主招生资格；若三个 问题均回答正确且笔试成绩在270分以上，则获A类资格；其它情况下获B类资格．现已知某中学有三人获得面试资格，且仅有一人笔试成绩为270分以上，在回答两个面试问题时，两人对每一个问题正确回答的概率均为
    12
    ，求恰有一位同学获得该高校B类资格的概率．

    查看答案和解析>>

    （2013•郑州一模）某高校组织自主招生考试，共有2000名优秀学生参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成八组：第一组[195，205），第二组[205，215），…，第八组[265，275]．如图是按上述分组方法得到的频率分 布直方图，且笔试成绩在260分（含260分）以上的同学进入面试．
    （I）估计所有参加笔试的2 000名学生中，参加 面试的学生人数；
    （II）面试时，每位考生抽取三个问题，若三个问题全答错，则不能取得该校的自主招生资格；若三个问题均回答正确且笔试成绩在270分以上，则获A类资格；其它情况下获B类资格．现已知某中学有三人获得面试资格，且仅有一人笔试成绩为270分以上，在回答三个面试问题时，三人对每一个问题正确回答的概率均为
    12
    ，用随机变量X表示该中学获得B类资格的人数，求X的分布列及期望EX．

    查看答案和解析>>

    （09年潍坊一模文）(12分)

      某中学组建了A、B、C、D、E五个不同的社团组织，为培养学生的兴趣爱好，要求每个学生必须参加，且只能参加一个社团．假定某班级的甲、乙、丙三名学生对这五个社团的选择是等可能的．

        (I)求甲、乙、丙三名学生参加五个社团的所有选法种数；

        (Ⅱ)求甲、乙、丙三人中至少有两人参加同一社团的概率；

        (Ⅲ)设随机变量为甲、乙、丙这三个学生参加A社团的人数，求的分布列与

    数学期望．

    查看答案和解析>>

    (本题满分12分） 为了了解某中学学生的体能情况，体育组决定抽样三个年级部分学生进行跳绳测试，并将所得的数据整理后画出频率分布直方图（如图5）.已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数是5.

    (1) 求第四小组的频率和参加这次测试的学生人数；

    (2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？

    (3) 参加这次测试跳绳次数在100次以上为优秀，试估计该校此年级跳绳成绩的优秀率是多少？

     

    查看答案和解析>>

    实验中学的三名学生甲、乙、丙参加某大学自主招生考核测试，在本次考核中只有合格和优秀两个等次，若考核为合格，则授予10分降分资格；考核优秀，授予20分降分资格．假设甲乙丙考核为优秀的概率分别为
    2
    3
    、
    2
    3
    、
    1
    2
    ，他们考核所得的等次相互独立．
    （1）求在这次考核中，甲乙丙三名同学中至少有一名考核为优秀的概率．
    （2）记在这次考核中甲乙丙三名同学所得降分之和为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．

    查看答案和解析>>


    同步练习册答案