
题目列表(包括答案和解析)
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数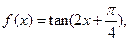 ,
,
(Ⅰ)求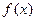 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设 ,若
,若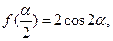 求
求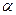 的大小.
的大小.
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数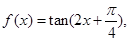 ,
,
(Ⅰ)求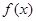 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设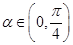 ,若
,若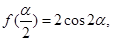 求
求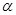 的大小.
的大小.
(本小题满分14分)甲、乙两间商店购进同一种商品的价格均为每件30元,销售价均为每件50元.根据前5年的有关资料统计,甲商店这种商品的年需求量![]() 服从以下分布:
服从以下分布:
|
| 10 | 20 | 30 | 40 | 50 |
|
| 0.15 | 0.20 | 0.25 | 0.30 | 0.10 |
乙商店这种商品的年需求量![]() 服从二项分布
服从二项分布![]() .
.
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理;乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推.今年甲、乙两间商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
(本小题满分15分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.

(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(本小题满分15分) 已知函数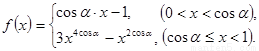 (其中
(其中
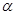 为锐角三角形的内角)且满足
为锐角三角形的内角)且满足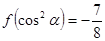 .
.
(1)求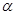 的值;
的值;
(2)若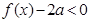 恒成立,求
恒成立,求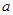 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com