(2006黄冈模拟)由原点O向三次曲线引切线，切于点(O、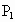两点不重合)，再由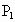引此曲线的切线，切于点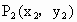(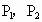不重合)，如此继续下去，得到点．

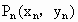(1)求；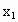

(2)求与满足的关系式；

(3)若a＞0，试判断与a的大小关系并说明理由．

由原点O向三次曲线y=x³-3ax²（a≠0）引切线，切点为P₁（x₁，y₁）（O，P₁两点不重合），再由P₁引此曲线的切线，切于点P₂（x₂，y₂）（P₁，P₂不重合），如此继续下去，得到点列：{P_n（x_n，y_n）}
（1）求x₁；
（2）求x_n与x_n+1满足的关系式；
（3）若a＞0，试判断x_n与a的大小关系，并说明理由

由原点O向三次曲线y=x³－3ax²＋b x (a≠0)引切线,切于不同于点O的点，再由P₁引此曲线的切线，切于不同于的点,如此继续地作下去，……,得到点列{ },试回答下列问题:

(1)求x₁;

(2)求x _n与x _n+1的关系;

(3)若a>0,求证:当n为正偶数时, x _n<a;当n为正奇数时, x _n>a.