
题目列表(包括答案和解析)
课本中推导点到直线的距离公式时是用的什么方法?你还能用哪些方法推导出来?
 如图,类比直线方程的截距式和点到直线的距离公式,则点H(4,2,1)到平面ABC的距离是
如图,类比直线方程的截距式和点到直线的距离公式,则点H(4,2,1)到平面ABC的距离是32
| ||
| 61 |
32
| ||
| 61 |
(08年西工大附中)如图,在直角坐标系中,O为坐标原点,直线![]() ⊥x轴于点C,
⊥x轴于点C, ![]() ,
,![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍![]()
(I)求点![]() 的轨迹方程;
的轨迹方程;
(II)设点K为点![]() 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线![]() 交点
交点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 与点K均不重合),且满足
与点K均不重合),且满足![]()
![]() 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
(Ⅲ)在(II)的条件下,动点![]() 满足
满足![]() ,求直线
,求直线![]() 的斜率的取值范围
的斜率的取值范围![]()

如图,在直角坐标系中,O为坐标原点,直线![]() ⊥x轴于点C,
⊥x轴于点C, ![]() ,
,![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍![]()
(I)求点![]() 的轨迹方程;
的轨迹方程;
(II)设点K为点![]() 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线![]() 交点
交点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 与点K均不重合),且满足
与点K均不重合),且满足![]()
![]() 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
(Ⅲ)在(II)的条件下,动点![]() 满足
满足![]() ,求直线
,求直线![]() 的斜率的取值范围
的斜率的取值范围![]()
观察下图,类比直线方程的截距式和点到直线的距离公式,点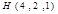 到平面
到平面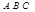 的距离是 .
的距离是 .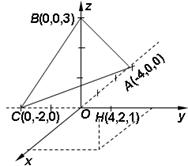
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com