
题目列表(包括答案和解析)
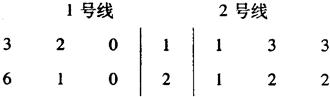
| 时间(天) | 15~25 | 25~35 | 35~45 | 45~55 | 55~65 |
| 1号线生产一台合格的该大型设备的频率 | 0.1 | 0.15 | 0.45 | 0.2 | 0.1 |
| 1号线生产一台合格的该大型设备的频率 | 0 | 0.25 | 0.4 | 0.3 | 0.05 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
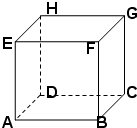 设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题:
设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题:平面上画了两条平行且相距2a的平行线.把一枚半径r<a的硬币任意投掷在这个平面上,求硬币不与任一条平行线相碰的概率.
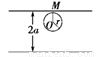
(本小题满分8分)
设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题: 
(1)若爬了两条线段(线段可以重复爬行),写出蚂蚁经过的所有路径;
(2)若爬了两条线段(线段可以重复爬行),蚂蚁停在顶点C的概率是多少?
(3)若爬了三条线段(线段可以重复爬行),蚂蚁停在顶点G的概率是多少?

对于上面给出的四个图象,以下说法正确的是
A.①反映了建议(2),③反映了建议(1) B.①反映了建议(1),③反映了建议(2)
C.②反映了建议(1),③反映了建议(2) D.④反映了建议(1),④反映了建议(1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com