(本题满分16分) 本题共有3个小题，第1小题满分7分，第2小题满分7分,第3小题满分2分. 

设直线交椭圆于两点，交直线于点．

（1）若为的中点，求证:；

（2）写出上述命题的逆命题并证明此逆命题为真；

（3）请你类比椭圆中（1）、（2）的结论，写出双曲线中类似性质的结论（不必证明）．

 

 （由理科第三册§1.3（3）P25练习第2题，文科第三册§1.1（2）P8第2题类比编制）某校高一、高二、高三共有学生4000人，三个年级的人数之比是32:33:35，用分层抽样的方法从所有学生中抽取一个容量为200的样本，高一、高二、高三各抽取的人数依次是（　　）

A．65、66、69　　　　　　　　　　　B．64、66、70

C．62、68、70　　　　　　　　　　　D．63、68、69

 

已知首项为x₁的数列{x_n}满足x_n+1=

axn

xn+1

（a为常数）．
（1）若对于任意的x₁≠-1，有x_n+2=x_n对于任意的n∈N^*都成立，求a的值；
（2）当a=1时，若x₁＞0，数列{x_n}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{x_n}由其首项x₁确定，当a=2时，通过对数列{x_n}的探究，写出“{x_n}是有穷数列”的一个真命题（不必证明）．说明：对于第3题，将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．

已知数列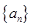的通项公式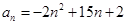，则此数列的最大项是（    ）

A．第1项   B．第3项   C．第4项   D．第7项

 

（本小题满分１２分）某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30)，第2组[30，35)，第3组[35，40)，第4组[40，45)，第5组[45，50]，得到的频率分布直方图如右图所示．

(1)下表是年龄的频数分布表，求正整数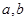的值；

区间	[25，30)	[30，35)	[35，40)	[40，45)	[45，50]
人数	50	50		150

 

 

 

 

 

(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人，年龄在第1,2,3组的人数分别是多少？

(3)在(2)的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．