（08年南昌市一模理）（12分）已知函数f (x) =lnx,g(x) =，（a为常数），若直线l与y =f(x), y =g(x)的图象都相切，且l与y = f(x)的图象相切的切点的横坐标为1.

（1）求直线l的方程及a的值；

（2） 当 2 ≤m <时,求h(x)= f(x)―f(x)[2g(x)- m +1]在[,2]上的最大值.

（本小题满分12分）向量a=（sinωx+cosωx，1），b=（f（x），simωx），其中0<ω<l，且a∥b．将f（x）的图象沿x轴向左平移个单位，沿y轴向下平移个单位，得到g（x）的图象，已知g（x）的图象关于（，0）对称   （I）求ω的值； （Ⅱ）求g（x）在[0，4π]上的单调递增区间．

（08年上虞市质检一理）已知椭圆C₁： (0<a<,0<b<2)与椭圆C₂：有相同的焦点. 直线L：y=k(x+1)与两个椭圆的四个交点，自上而下顺次记为A、B、C、D.

(I)求线段BC的长（用k和a表示）;

(II)是否存在这样的直线L,使线段AB、BC、CD的长按此顺序构成一个等差数列.请说明详细的理由.

定义：已知函数f（x）与g（x），若存在一条直线y=kx +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx +b为曲线f（x）与g（x）的“左同旁切线”．已知

    （I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；

    （Ⅱ）设P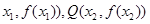（是函数 f（x）图象上任意两点，且0<x₁<x₂，若存在实数x₃>0，使得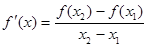．请结合（I）中的结论证明：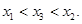

（09年山东质检）（12分）

向量a=（sinωx+cosωx，1），b=（f（x），simωx），其中0<ω<l，且a∥b．将f（x）的图象沿x轴向左平移个单位，沿y轴向下平移个单位，得到g（x）的图象，已知g（x）的图象关于（，0）对称

   （I）求ω的值；

   （Ⅱ）求g（x）在[0，4π]上的单调递增区间．