
题目列表(包括答案和解析)
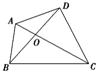 如图,四边形ABCD被两条对角线分成四个小三角形,现有4种不同颜色将它染色,使相邻三角形均不同色,求使△AOB与△COD 同色且△BOC与△AOD也同色的概率( )
如图,四边形ABCD被两条对角线分成四个小三角形,现有4种不同颜色将它染色,使相邻三角形均不同色,求使△AOB与△COD 同色且△BOC与△AOD也同色的概率( )为配合新课程的实施,乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛,共有1500名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
|
组别 |
分 组 |
频 数 |
频率 |
|
1 |
49.5~59.5 |
60 |
0.12 |
|
2 |
59.5~69.5 |
120 |
0.24 |
|
3 |
69.5~79.5 |
180 |
0.36 |
|
4 |
79.5~89.5 |
130 |
|
|
5 |
89.5~99.5 |
|
0.02 |
|
合 计 |
|
1.00 |
解答下列问题:
(1)在这个问题中,总体是 ,样本是 ,
样本容量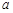 =
;
=
;
(2)第四小组的频率 =
;
=
;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计此次竞赛获一等奖的人数.
A.与A同号,与B同号 B.与A同号,与B异号
C.与A异号,与B同号 D.与A异号,与B异号
A.与A同号,与B同号 B.与A同号,与B异号
C.与A异号,与B同号 D.与A异号,与B异号




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com