
题目列表(包括答案和解析)
(理)(本题8分)甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(1)求只进行两局比赛,甲就取得胜利的概率;
(2)求只进行两局比赛,比赛就结束的概率;
(3)求甲取得比赛胜利的概率.
20、(文)(本小题8分)甲、乙两人做定点投篮,投篮者若投中则继续投篮,否则由对方投篮,第一次甲投篮,已知甲、乙每次投篮命中的概率分别为 、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.
(1)求第三次由乙投篮的概率;
(2)求前4次投篮中各投两次的概率.
(理)(本题8分)甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(1)求只进行两局比赛,甲就取得 胜利的概率;
胜利的概率;
(2)求只进行两局比赛,比赛就结束的概率;
(3)求甲取得比赛胜利的概率.
20、(文)(本小题8分)甲、乙两人做定点投篮,投篮者若投中则继续投篮,否则由对方投篮,第一次甲投篮,已知甲、乙每次投篮命中的概率分别为 、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.
(1)求第三次由乙投篮的概率;
(2)求前4次投篮中各投两次的概率.
(文)(本小题8分)
如图,在四棱锥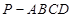 中,
中, 平面
平面 ,
, ,
, ,
,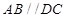 ,
,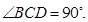
(1)求证: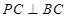 ;
;
(2)求点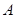 到平面
到平面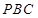 的距离
的距离
证明:(1) 平面
平面 ,
,
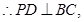 又
又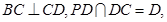
 平面
平面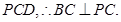 (4分)
(4分)
(2)设点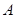 到平面
到平面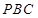 的距离为
的距离为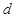 ,
,
 ,
, ,
,
求得 即点
即点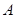 到平面
到平面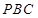 的距离为
的距离为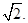 (8分)
(8分)
(其它方法可参照上述评分标准给分)
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
(08年山东卷文)(本小题满分12分)现有8名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语,![]() 通晓俄语,
通晓俄语,![]() 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求![]() 被选中的概率;
被选中的概率;
(Ⅱ)求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com