
题目列表(包括答案和解析)
已知抛物线y2=2px(p>0)与双曲线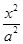 -
-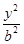 =1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,AF⊥x轴,若直线L是双曲线的一条渐近线,则直线L的倾斜角所在的区间可能为( )
=1(a>0,b>0)有相同的焦点F,点A是两曲线的一个交点,AF⊥x轴,若直线L是双曲线的一条渐近线,则直线L的倾斜角所在的区间可能为( )
A.(0,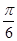 )
B.(
)
B.(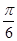 ,
,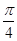 )
C.(
)
C.(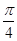 ,
,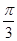 )
D.(
)
D.(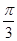 ,
,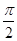 )
)
设x,y满足约束条件 ,若目标函数z ="ax+by"
(a>0, b>0)的最大值为8,点P为曲线
,若目标函数z ="ax+by"
(a>0, b>0)的最大值为8,点P为曲线 上动点,则点P到点(a,b)的最小距离为
上动点,则点P到点(a,b)的最小距离为
A.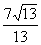 B.O C.
B.O C.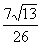 D.1
D.1
(04年上海卷文)(18分)
设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点, 且a1=![]() 2, a2=
2, a2=![]() 2, …, an=
2, …, an=![]() 2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
(1) 若C的方程为![]() -y2=1,n=3. 点P1(3,0) 及S3=162, 求点P3的坐标;
-y2=1,n=3. 点P1(3,0) 及S3=162, 求点P3的坐标;
(只需写出一个)
(2) 若C的方程为y2=2px(p≠0). 点P1(0,0), 对于给定的自然数n, 证明:
(x1+p)2, (x2+p)2, …,(xn+p)2成等差数列;
(3) 若C的方程为![]() (a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.
(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.
(本小题满分14分)
(1)已知等差数列{an}的前n项和为Sn,若m+n=s+t(m,n,s,t∈N*,且m≠n,s≠t),证明; =
=  ;
;
(2)注意到(1)中Sn与n的函数关系,我们得到命题:设抛物线x2=2py(p>0)的图像上有不同的四点A,B,C,D,若xA,xB,xC,xD分别是这四点的横坐标,且xA+xB=xC+xD,则AB∥CD,判定这个命题的真假,并证明你的结论
(3)我们知道椭圆和抛物线都是圆锥曲线,根据(2)中的结论,对椭圆 +
+ =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.
设双曲线 (a>0,b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为P.若|PF|=5,则双曲线的渐近线方程为____.
(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为P.若|PF|=5,则双曲线的渐近线方程为____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com