21．附加题: (本题分值6分, 计入总分, 但本题与前20题得分之和不超过100分.) 解: (1)顶点C是以A.B为圆心|AB|为半径的两圆在第一象限的交点. 由圆A: 2 + y2 = a——青夏教育精英家教网—

21．附加题: (本题分值6分, 计入总分, 但本题与前20题得分之和不超过100分.) 解: (1)顶点C是以A.B为圆心|AB|为半径的两圆在第一象限的交点. 由圆A: 2 + y2 = a2 + b2 , 圆B: x2 + 2 = a2 + b2 . 解得 x = , y = . ∴C(. ) △ABC含于正方形D内.即三顶点A.B.C含于区域D内时. ∴ 这就是的约束条件. 其图形为右图的六边形. ∵a > 0 , b > 0 , ∴图中坐标轴上的点除外. 4分 (2)∵△ABC是边长为的正三角形, ∴ S = ( a2 + b2 ) 在(1)的条件下, 当S取最大值等价于六边形图形中的点到原点的距离最大, 由六边形中P.Q.R相应的OP.OQ.OR的计算. OP2 = OR2 = 12 + ( 2 – )2 = 8 – 4; OQ2 = 2( – 1)2 = 8 – 4. 知: 当 = ( 1, 2 –), 或(– 1, – 1), 或( 2 –, 1 )时, Smax =2– 3. 2分【查看更多】

已知圆A：（x-1）²+y²=4与x轴负半轴交于B点，过B的弦BE与y轴正半轴交于D点，且2BD=DE，曲线C是以A，B为焦点且过D点的椭圆．
（1）求椭圆的方程；
（2）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．
[本小问为附加题，分值5分]（3）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．

查看答案和解析>>

附加题(本题满分10分)

某厂生产某种零件,每个零件的成本为元,出厂单价定为元,该厂为鼓励销售部门订购,决定当一次订购量超过个时,每多订购一个，订购全部零件的出厂单价就降元,但实际出厂单价不能低于元．

（Ⅰ)当一次订购量为多少时，零件的实际出厂单价恰降为元？

（Ⅱ)当一次订购量为个，零件的实际出厂单价为元，写出函数的表达式.

（Ⅲ)当销售商一次订购个零件时,该厂获得的利润是多少元?如果订购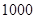个,利润是多少元?

查看答案和解析>>

(附加题)本题满分20分
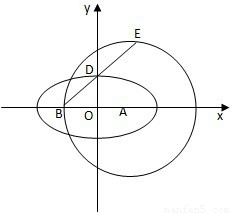
如图，已知抛物线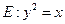与圆相交于A、B、C、D四个点。

（Ⅰ）求r的取值范围（Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标。

查看答案和解析>>

已知圆A：（x-1）²+y²=4与x轴负半轴交于B点，过B的弦BE与y轴正半轴交于D点，且2BD=DE，曲线C是以A，B为焦点且过D点的椭圆．
（1）求椭圆的方程；
（2）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．
[本小问为附加题，分值5分]（3）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值．

查看答案和解析>>

附加题：（本题共6分，附加题的得分直接加入总分，总分最高分不超过150分）
已知函数f（x）=lgsin（cosx）
（1）求y=f（x）的定义域；
（2）判断函数的奇偶性，并说明理由；
（3）求y=f（x）的单调区间．

查看答案和解析>>

练习册

高中

初中

小学