
题目列表(包括答案和解析)
(本小题满分12分)
已知直线![]() 所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
(1)求椭圆C的标准方程;
(2)已知圆O:![]() ,直线
,直线![]() :
:![]() ,当点
,当点![]() 在椭圆C上运动时,直线
在椭圆C上运动时,直线![]() 与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
(本小题满分12分)
已知直线![]() 所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
(1)求椭圆C的标准方程;
(2)已知圆O:![]() ,直线
,直线![]() :
:![]() ,当点
,当点![]() 在椭圆C上运动时,直线
在椭圆C上运动时,直线![]() 与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的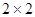 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为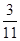 .
.
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
附: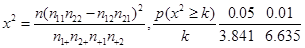 )
)
(本小题满分12分)已知顶点在坐标原点,焦点在 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点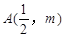 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦 ,
, ,求证:
,求证: 恒过定点
恒过定点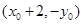 .(3)直线
.(3)直线 与抛物线交于
与抛物线交于 ,
, 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点 ,使得△
,使得△ 为以
为以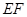 为斜边的直角三角形.
为斜边的直角三角形.
(本小题满分12分)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com