
题目列表(包括答案和解析)
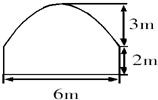 某隧道横断面由抛物线和矩形的三边组成,尺寸如图所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.
某隧道横断面由抛物线和矩形的三边组成,尺寸如图所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.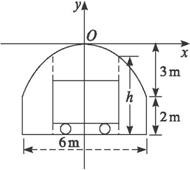
(本小题12分)
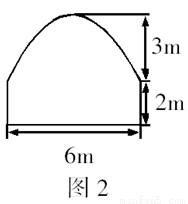
某隧道横断面由抛物线和矩形的三边组成,尺寸如图2所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.
(本小题12分)
某隧道横断面由抛物线和矩形的三边组成,尺寸如图2所示,某卡车载一集装箱,箱宽3m,车与箱共高4m,此车能否通过此隧道?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com