对于定义在D上的函数y=f(x),若同时满足.
①存在闭区间[a,b]⊆D,使得任取x
1∈[a,b],都有f(x
1)=c (c是常数);
②对于D内任意x
2,当x
2∉[a,b]时总有f(x
2)>c称f(x)为“平底型”函数.
(1)(理)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
,x∈[-2,+∞)是“平底型”函数,求m和n的值;
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件.

 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;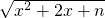 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;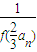 .
.