
题目列表(包括答案和解析)
已知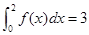 ,则
,则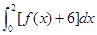 等于
( )
等于
( )
A、9 B、12 C、15 D、18
(2011-2012·安徽合肥一模)如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
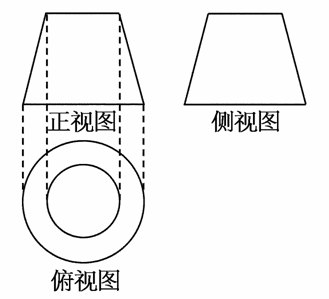
A.6π B.12π C.18π D.24π
四张卡片上分别标有数字“2”、“0”、“0”、“9”,其中“9”可当6使用,则由这四张卡片可组成不同的四位数的个数为( )
A.24 B.18 C.12 D.6
已知在平面直角坐标系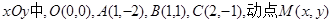 满足条件
满足条件
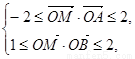 则
则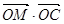 的最大值为( )
的最大值为( )
A.4 B.8 C.12 D.15
向量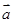 与
与 的夹角为120°,|
的夹角为120°,|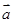 |=2,|
|=2,| |=5,则(2
|=5,则(2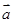 -
- )·
)·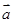 =( )
=( )
A.3 B.9 C.12 D.13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com