
题目列表(包括答案和解析)
选择题.
(1)
由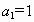 ,
,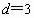 确定的等差数列
确定的等差数列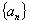 ,当
,当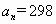 时,序号n等于
时,序号n等于
[
]|
(A)99 . |
(B)100 . |
(C)96 . |
(D)101 . |
(2)
一个蜂巢里有1只蜜蜂.第1天,它飞出去找回了5个伙伴;第2天,6只蜜蜂飞出去,各自找回了5个伙伴……如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中一共有( )只蜜蜂.[
]|
(A)55986 . |
(B)46656 . |
(C)216 . |
(D)36 . |
(3)
预测人口的变化趋势有多种方法,“直接推算法”使用的公式是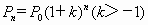 ,其中
,其中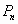 为预测期人口数,
为预测期人口数,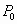 为初期人口数,k为预测期内年增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么在这期间人口数
为初期人口数,k为预测期内年增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么在这期间人口数
[
]|
(A) 呈上升趋势. |
(B) 呈下降趋势. |
(C) 摆动变化. |
(D) 不变. |
(4)
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的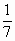 是较小的两份之和,问最小1份为
是较小的两份之和,问最小1份为
[
]|
(A) |
(B) |
(C) |
(D) |
A、
| ||
B、
| ||
C、
| ||
D、
|
| A、3×10-4 | B、3×10-5 | C、3×10-6 | D、3×10-7 |
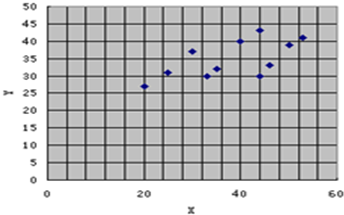 某次数学测试分为选择题与非选择题两部分,右边的散点图中每个点(X,Y)表示一位学生在这两部分的得分,其中X表示该生选择题得分,Y表示该生非选择题得分,设Z=X+Y表示该生的总分,现有11位学生的得分数据,根据散点图,下列判断正确的是( )
某次数学测试分为选择题与非选择题两部分,右边的散点图中每个点(X,Y)表示一位学生在这两部分的得分,其中X表示该生选择题得分,Y表示该生非选择题得分,设Z=X+Y表示该生的总分,现有11位学生的得分数据,根据散点图,下列判断正确的是( )(本小题满分12分)
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.试求出该考生:
(Ⅰ)得60分的概率;
(Ⅱ)得多少分的可能性最大?
(Ⅲ)所得分数![]() 的数学期望(用小数表示,精确到0.k^s*5#u01).
的数学期望(用小数表示,精确到0.k^s*5#u01).
(文科)投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是0,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(Ⅰ)求点P落在区域![]() 上的概率;
上的概率;
(Ⅱ)若以落在区域![]() 上的所有点为顶点作面积最大的多边形区域
上的所有点为顶点作面积最大的多边形区域![]() ,在区域
,在区域![]() 上随机撒一粒豆子,求豆子落在区域M上的概率.
上随机撒一粒豆子,求豆子落在区域M上的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com