(2)甲、乙两射手同时射击一目标，甲的命中率为0.65，乙的命中率为0.60，那么能否得出结论，目标被命中的概率等于0.65+0．60=1.25？为什么？

(3)一射手命中靶的内圈的概率是0.25，命中靶的其余部分的概率是0.50，那么能否得出结论，目标被命中的概率等于0.25+0.50=0.75？为什么？

(1)两人各掷一枚硬币，“同时出现正面”的概率可以算得为，由于“不出现正面”是上述事件的对立事件，所以它的概率等于1-=.这样计算对吗？为什么？

    (2)甲、乙两射手同时射击一目标，甲的命中率为0.65，乙的命中率为0.60，那么能否得出结论，目标被命中的概率等于0.65+0．60=1.25？为什么？

    (3)一射手命中靶的内圈的概率是0.25，命中靶的其余部分的概率是0.50，那么能否得出结论，目标被命中的概率等于0.25+0.50=0.75？为什么？

甲，乙，丙三人投篮，甲的命中率为p，乙，丙的命中率均为q（p，q∈（0，1））．现每人独立投篮一次，记命中的总次数为随机变量ξ．
（1）当时，求数学期望E（ξ）；
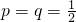（2）当p+q=1时，试用p表示ξ的数学期望E（ξ）．

(1)甲、乙两射手同时射击一目标,甲的命中率为0.65,乙的命中率为0.60,那么能否得出结论：目标被命中的概率等于0.65+0.60=1.25,为什么?

(2)一射手命中靶的内圈的概率是0.25,命中靶的其余部分的概率是0.50,那么能否得出结论：目标被命中的概率等于0.25+0.50=0.75,为什么?

(3)两人各掷一枚硬币,“同时出现正面”的概率可以算得为.由于“不出现正面”是上述事件的对立事件,所以它的概率等于,这样做对吗?说明道理.