
题目列表(包括答案和解析)
|
| x2 |
| 4 |
|
| π |
| 2 |
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
|
|
| α |
| α |
| β |
|
|
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.| 5 |
|
|
(本小题满分16分)已知函数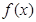 =
=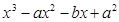 ,
,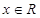 ,
,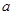 ,
,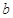 为常数。
为常数。
(1)若函数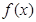 在
在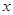 =1处有极值10,求实数
=1处有极值10,求实数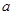 ,
,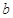 的值;
的值;
(2)若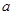 =0,(I)方程
=0,(I)方程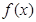 =2在
=2在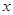 ∈[-4,4]上恰有3个不相等的实数解,求实数
∈[-4,4]上恰有3个不相等的实数解,求实数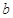 的取值范围;(II)不等式
的取值范围;(II)不等式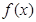 +2
+2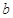 ≥0对
≥0对
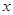 ∈[1,4]恒成立,求实数
∈[1,4]恒成立,求实数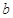 的取值范围。
的取值范围。
(本小题满分16分)
已知函数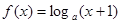 ,
,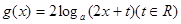 ,其中
,其中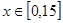 ,
,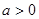 ,且
,且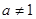 。
。
(1)若1是关于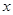 的方程
的方程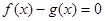 的一个解,求
的一个解,求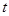 的值;
的值;
(2)当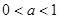 时,不等式
时,不等式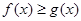 恒成立,求
恒成立,求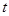 的取值范围;
的取值范围;
(3)当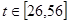 时,函数
时,函数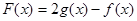 的最小值为
的最小值为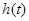 ,求
,求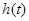 的解析式.
的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com