（本小题共13分）

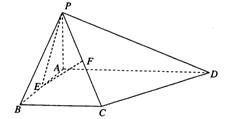
    如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

∠BAD=90°，AD＞BC，E，F分别为棱AB，PC的中点.

   （I）求证：PE⊥BC；

   （II）求证：EF//平面PAD.

（本小题共13分）

某小区在一次对20岁以上居民节能意识的问卷调查中，随机抽取了100份问卷进行统计，得到相关的数据如下表：

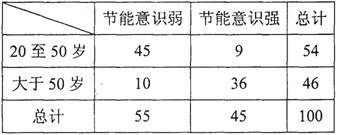
    (1)由表中数据直观分析，节能意识强弱是否与人的年龄有关？

    (2)据了解到，全小区节能意识强的人共有350人，估计这350人中，年龄大于50岁的有多少人？

    (3)按年龄分层抽样，从节能意识强的居民中抽5人，再从这5人中任取2人，求恰有1人年龄在20至50岁的概率。

（本小题共13分）[来源:Z,xx,k.Com]

在一次考试中共有8道选择题，每道选择题都有4个选项，其中有且只有一个选项是正确的.某考生有4道题已选对正确答案，其余题中有两道只能分别判断2个选项是错误的，还有两道题因不理解题意只好乱猜.

(Ⅰ) 求该考生8道题全答对的概率；

(Ⅱ)  若评分标准规定：“每题只选一个选项，选对得5分，不选或选错得0分”，求该考生所得分数的分布列.

. （本小题共13分）

         在平面直角坐标系xOy中，经过点（0, ）且斜率为k的直线l与椭圆 有两个不同的交点P和Q.

(Ⅰ)求k的取值范围；

(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k，使得向量与共线？如果存在，求出k的值；如果不存在，请说明理由.

（本小题共13分）

已知每项均是正整数的数列：，其中等于的项有个，

设 ， .

（Ⅰ）设数列，求；

（Ⅱ）若数列满足，求函数的最小值.