练习册

  • 练习册
  • 试题
    10．设函数f(x)＝+. (1)求函数f(x)的定义域, (2)判断函数f(x)的单调性.并给出证明, (3)已知函数f(x)的反函数f-1(x).问函数y＝f-1(x)的图象与x轴有交点吗?若有.求出交点坐标,若无交点.说明理由． 解:(1)由3x+5≠0且＞0.解得x≠-且-＜x＜．取交集得-＜x＜． (2)令(x)＝3x+5.随着x增大.函数值减小.所以在定义域内是减函数, ＝-1+随着x增大.函数值减小.所以在定义域内是减函数． 又y＝lgx在定义域内是增函数.根据复合单调性可知.y＝是减函数.所以f(x)＝+是减函数． (3)因为直接求f(x)的反函数非常复杂且不易求出.于是利用函数与其反函数之间定义域与值域的关系求解． 设函数f(x)的反函数f-1(x)与工轴的交点为(x0.0)．根据函数与反函数之间定义域与值域的关系可知.f(x)与y轴的交点是(0.x0).将(0.x0)代入f(x).解得x0＝．所以函数y＝f-1(x)的图象与x轴有交点.交点为(.0). 欢迎访问 【查看更多】

     

    题目列表(包括答案和解析)

    设函数f(x)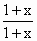＝，若对于不等于±1的实数y、z，有等式f(y)＋f(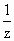－)＝2成立．

    (1)求函数y＝g(z)及其定义域；

    (2)求方程g(z)＝g(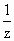)的解集．

    查看答案和解析>>

    设函数f(x)＝1＋(1＋a)－x2－x3，其中a＞0

    (1)讨论f(x)在其定义域上的单调性；

    (2)当x∈[0，1]时，求f(x)取得最大值和最小值时的x的值．

    查看答案和解析>>

    设函数f(x)＝a2x2(a＞0)，g(x)＝blnx．

    (Ⅰ)将函数y＝f(x)图象向右平移一个单位即可得到函数y＝φ(x)的图象，试写出y＝φ(x)的解析式及值域；

    (Ⅱ)关于x的不等式(x－1)2＞f(x)的解集中的整数恰有3个，求实数a的取值范围；

    (Ⅲ)对于函数f(x)与g(x)定义域上的任意实数x，若存在常数k，m，使得f(x)≥kx＋m和g(x)≤kx＋m都成立，则称直线y＝kx＋m为函数f(x)与g(x)的“分界线”．设a＝，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

    查看答案和解析>>

    设函数f(x)＝ax－(1＋a2)x2，其中a>0，区间I＝{x|f(x)>0}．
    (1)求I的长度(注：区间(α，β)的长度定义为β－α)；
    (2)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I的长度的最小值．

    查看答案和解析>>

    设函数f(x)＝ax－(1＋a2)x2，其中a>0，区间I＝{x|f(x)>0}．
    (1)求I的长度(注：区间(α，β)的长度定义为β－α)；
    (2)给定常数k∈(0,1)，当1－k≤a≤1＋k时，求I长度的最小值．

    查看答案和解析>>


    同步练习册答案