练习册

  • 练习册
  • 试题
    对n个向量.若存在n个不全为零的实数k1.k2.--.kn.使得＝0.则称向量是“线性相关 的.按此规定.能说明平面向量.. “线性相关 的实数k1.k2.k3依次可以取 -2.2.1 . 【查看更多】

     

    题目列表(包括答案和解析)

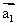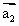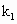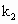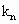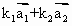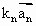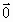    若对n个向量，，…存在n个不全为零的实数，，…，使得…＋＝成立，则称向量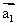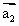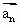，，…，为“线性相关”．依此规定，能说明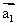＝(1，－1)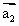，＝(1，－1)，＝(2，2)“线性相关”的实数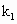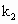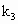，，依次可以取________(写出一组数值即可，不必考虑所有情况)

    查看答案和解析>>

    对n个向量
    a1
    ，
    a2
    ，…
    an
    ，如果存在不全为零的实数k1，k2…kn使得k1
    a1
    +k2
    a2
    +…+kn
    an
    =0    ，则称
    a1
    ，
    a2
    ，…
    an
    线性相关．若已知
    a1
    =(1，1)    ，
    a2
    =(3，-2)    ，
    a3
    =(3，-7)    是线性相关的，则k1：k2：k3=
    3：（-2）：1
    3：（-2）：1
    ．

    查看答案和解析>>

    若对n个向量，存在n个不全为零的实数k1，k2，…，kn，使得=成立，则称向量为“线性相关”.依此规定，若 =(1,0), =(1,－1), =(2,2) “线性相关”，则的比值是               

     

    查看答案和解析>>

    对n个向量
    a1
    ，
    a2
    ，…
    an
    ，如果存在不全为零的实数k1，k2…kn使得k1
    a1
    +k2
    a2
    +…+kn
    an
    =0    ，则称
    a1
    ，
    a2
    ，…
    an
    线性相关．若已知
    a1
    =(1，1)    ，
    a2
    =(3，-2)    ，
    a3
    =(3，-7)    是线性相关的，则k1：k2：k3=______．

    查看答案和解析>>

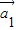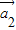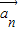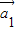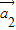    若对n个向量•，…存在n个不全为零的实数k1，k2，…，kn，使得k1+k2+…，kn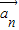=成立，则称向量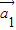、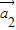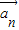，…为“线性相关”．依此规定，能说明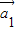=（1，2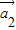），=（1，-1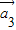），=（2，2）“线性相关”的实数k1，k2，k3依次可以取     （写出一组数值即中，不必考虑所有情况）．

    查看答案和解析>>


    同步练习册答案