
题目列表(包括答案和解析)
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分) A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与轴正半轴的交点, 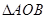 为等腰直角三角形。记
为等腰直角三角形。记 (1)若A点的坐标为
(1)若A点的坐标为 ,求
,求
 的值 (2)求
的值 (2)求 的取值范围。
的取值范围。
 |
(本题14分) 已知等差数列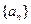 的前
的前 项和为
项和为 (
(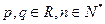 )
)
(1)求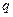 的值;
的值;
(2)若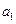 与
与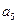 的等差中项为18,
的等差中项为18,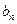 满足
满足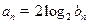 ,求数列
,求数列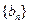 的前
的前 项和
项和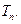
(本小题14分)已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].(1)求g(x)的解析式;(2)判断g(x)的单调性.
(本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
|
|
14 |
16 |
18 |
20 |
22 |
|
|
12 |
10 |
7 |
5 |
3 |
(1)画出 关于
关于 的散点图
的散点图
(2)用最小二乘法求出回归直线方程
(3)计算 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com