.(本小题满分12分)

已知以函数f(x)＝mx³－x的图象上一点N(1，n)为切点的切线倾斜角为.

(1)求m、n的值；

(2)是否存在最小的正整数k，使得不等式f(x)≤k－1995，对于x∈[－1,3]恒成立？若存在，求出最小的正整数k，否则请说明理由．

.(本小题满分12分)
已知以函数f(x)＝mx³－x的图象上一点N(1，n)为切点的切线倾斜角为.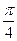
(1)求m、n的值；
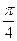(2)是否存在最小的正整数k，使得不等式f(x)≤k－1995，对于x∈[－1,3]恒成立？若存在，求出最小的正整数k，否则请说明理由．

（本小题满分12分）一名高二学生盼望进入某名牌大学学习，不放弃能考入该大学的任何一次机会。已知该大学通过以下任何一种方式都可被录取：

① 2010年2月国家数学奥赛集训队考试通过（集训队从2009年10月省数学竞赛壹等奖获得者中选拔，通过考试进入集训队则能被该大学提前录取）；

② 2010年3月自主招生考试通过并且2010年6月高考分数达重点线；

③ 2010年6月高考达到该校录取分数线（该校录取分数线高于重点线）。

该名考生竞赛获省一等奖、自主招生考试通过、高考达重点线、高考达该校分数线等事件的概率如下表：

如果数学竞赛获省一等奖，该学生估计自己进入国家集训队的概率是0.4。

（1）求该学生参加自主招生考试的概率；

（2）求该学生参加考试次数的分布列与数学期望；

（3）求该学生被该大学录取的概率。