设定义在R上的偶函数f(x)，其图像关于点(1，0)对称，并且x∈[2，4]时，f(x)＝(3－x)³．

(Ⅰ)证明：f(x)＋f(2－x)＝0(x∈R)；

(Ⅱ)证明f(x)－f(x＋4)＝0(x∈R)，并写出f(x)的最小正周期；

(Ⅲ)求f(x)在[－2，2]上的解析式，并写出f(x)在R上的单调递增区间(不必证明单调性)．

求圆心在直线3x＋4y－1＝0上且过两圆x²＋y²－x＋y－2＝0与x²＋y²＝5的交点的圆的方程．

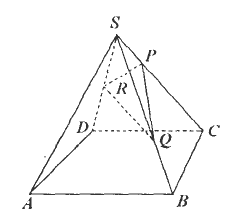
如图，正四棱锥S－ABCD中，P、Q、R分别在SC、SB、SD上，且＝，＝＝2，求证：SA∥平面PQR．

某厂在一个空间容积为2000m³的密封车间内生产某种化学药品．开始生产后，每满60分钟会一次性释放出有害气体am³，并迅速扩散到空气中．每次释放有害气体后，车间内的净化设备随即自动工作20分钟，将有害气体的含量降至该车间内原有有害气体含量的r％，然后停止工作，待下一次有害气体释放后再继续工作．安全生产条例规定：只有当车间内的有害气体总量不超过1.25am³时才能正常进行生产．

(Ⅰ)当r＝20时，该车间能否连续正常生产6.5小时？请说明理由；

(Ⅱ)能否找到一个大于20的数据r，使该车间能连续正常生产6.5小时？请说明理由；

(Ⅲ)(本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分)

已知该净化设备的工作方式是：在向外释放出室内混合气体(空气和有害气体)的同时向室内放入等体积的新鲜空气．已知该净化设备的换气量是200m³／分，试证明该设备连续工作20分钟能够将有害气体含量降至原有有害气体含量的20％以下．(提示：我们可以将净化过程划分成n次，且n趋向于无穷大．)