
题目列表(包括答案和解析)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
|
| A.1.15 | B.1.25 | C.0.75 | D.2.5 |
下表是某同学记载的5月1日至5月12日每天北京市SARS病患者。治愈者的数据,以及根据这些数据绘制出的散点图。
|
日期 |
5.1 |
5.2 |
5.3 |
5.4 |
5.5 |
5.6 |
|
人数 |
100 |
109 |
115 |
118 |
121 |
134 |
|
日期 |
5.7 |
5.8 |
5.9 |
5.10 |
5.11 |
5.12 |
|
人数 |
141 |
152 |
168 |
175 |
186 |
203 |
下列说法:
①根据此散点图,可以判断日期与人数具有线性相关关系;
②若日期与人数具有线性相关关系,则相关系数r与临界值
r0.05应满足|r|>r0.05;
③根据此散点图,可以判断日期与人数具有-次函数关系。
其中正确的个数为( )
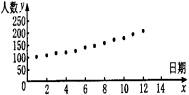
A.0 B.1 C.2 D.3
2003年春季.我国部分地SARS流行,党和政府采取果断措施.防治结合。很快使病情得到控制。
下表是某同学记载的5月1日至5月12日每天北京市SARS病患者。治愈者的数据,以及根据这些数据绘制出的散点图。
|
日期 |
5.1 |
5.2 |
5.3 |
5.4 |
5.5 |
5.6 |
|
人数 |
100 |
109 |
115 |
118 |
121 |
134 |
|
日期 |
5.7 |
5.8 |
5.9 |
5.10 |
5.11 |
5.12 |
|
人数 |
141 |
152 |
168 |
175 |
186 |
203 |
下列说法:
①根据此散点图,可以判断日期与人数具有线性相关关系;
②若日期与人数具有线性相关关系,则相关系数r与临界值
r0.05应满足|r|>r0.05;
③根据此散点图,可以判断日期与人数具有-次函数关系。
其中正确的个数为( )
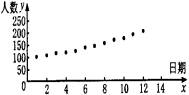
A.0 B.1 C.2 D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com