
题目列表(包括答案和解析)
求由抛物线 与直线
与直线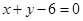 及
及 所围成图形的面积.
所围成图形的面积.
【解析】首先利用已知函数和抛物线作图,然后确定交点坐标,然后利用定积分表示出面积为 ,所以得到
,所以得到 ,由此得到结论为
,由此得到结论为
解:设所求图形面积为 ,则
,则

 =
= .即所求图形面积为
.即所求图形面积为 .
.

(本小题共14分)
已知![]() 为数列
为数列![]() 的前n项和,且
的前n项和,且![]()
(I)求证:数列![]() 为等比数列;
为等比数列;
(II)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(III)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:![]() 。
。
用二分法设计一个求方程x2-2=0的正近似根的算法(设所求近似根与精确解的差的绝对值不超过0.005).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com