
题目列表(包括答案和解析)
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
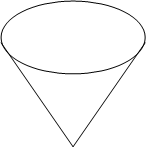
如下图为一圆锥形容器,其底面圆直径等于圆锥母线长,水以每分钟9.3升的速度注入容器内,则注入水的高度在![]() 分钟时的瞬时变化率约为(注:π≈3.1)( )分米/分
分钟时的瞬时变化率约为(注:π≈3.1)( )分米/分
A.9
B.0.97
C.0.33
D.27
(本题满分13分)
甲、乙两人同时参加某电台举办的有奖知识问答。约定甲,乙两人分别回答4个问题,答对一题得1分,不答或答错得0分,4个问题结束后以总分决定胜负。甲,乙回答正确的概率分别是 和
和 ,且不相互影响。求:
,且不相互影响。求:
(1) 甲回答4次,至少得1分的概率;
(2) 甲恰好以3分的优势取胜的概率。
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
(本题满分13分)
甲、乙两人同时参加某电台举办的有奖知识问答。约定甲,乙两人分别回答4个问题,答对一题得1分,不答或答错得0分,4个问题结束后以总分决定胜负。甲,乙回答正确的概率分别是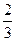 和
和 ,且不相互影响。求:
,且不相互影响。求:
(1) 甲回答4次,至少得1分的概率;
(2) 甲恰好以3分的优势取胜的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com