
题目列表(包括答案和解析)
(本小题满分13分)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第![]() 层第
层第![]() 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为![]() .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求![]() 的值,并猜想
的值,并猜想![]() 的表达式.(不必证明)
的表达式.(不必证明)
 (Ⅱ)设小弹子落入第6层第
(Ⅱ)设小弹子落入第6层第![]() 个竖直通道得到分数为
个竖直通道得到分数为![]() ,
,
其中![]() ,试求
,试求![]() 的分布列及数学期望.
的分布列及数学期望.
(本小题满分14分)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第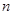 层第
层第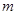 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为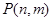 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求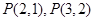 的值,并猜想
的值,并猜想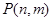 的表达式.(不必证明)
的表达式.(不必证明)
(Ⅱ)设小弹子落入第6层第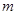 个竖直通道得到分数为
个竖直通道得到分数为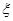 ,其中
,其中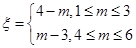 ,试求
,试求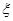 的分布列及数学期望.
的分布列及数学期望.
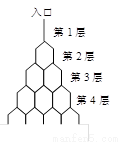
(本小题满分12分)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,……,依次类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是 .记小球遇到第
.记小球遇到第 行第
行第 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为 .
.
(Ⅰ)求 ,
, 的值,并猜想
的值,并猜想 的表达式(不必证明);
的表达式(不必证明);
(Ⅱ)已知 ,设小球遇到第6行第
,设小球遇到第6行第 个障碍物(从左至右)上顶点时,
个障碍物(从左至右)上顶点时,
得到的分数为 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,……,依次类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是 .记小球遇到第
.记小球遇到第 行第
行第 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为 .
.
(Ⅰ)求 ,
, 的值,并猜想
的值,并猜想 的表达式(不必证明);
的表达式(不必证明);
(Ⅱ)已知 ,设小球遇到第6行第
,设小球遇到第6行第 个障碍物(从左至右)上顶点时,
个障碍物(从左至右)上顶点时,
得到的分数为 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.

(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是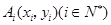 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
(1) 若点 为抛物线
为抛物线
 准线上
准线上
一点,点 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线
 经
经
过该抛物线的焦点,证明 .
.
(2)若点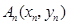 要么落在
要么落在 所表示的曲线上,
所表示的曲线上,
要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,
,
试写出 (不需证明);
(不需证明);
(3)若点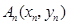 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求 的表达式.
的表达式.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com