
题目列表(包括答案和解析)
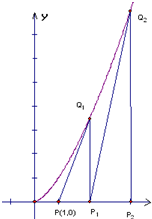 如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.| n |
| k-1 |
| n |
 |
| i=1 |
| i |
| ai |
| n |
 |
| i=1 |
(08年咸阳市一模) (14分)如图,过点P(1,0)作曲线C: ![]() 的切线,切点为
的切线,切点为![]() ,设
,设![]() 点在x轴上的投影是点
点在x轴上的投影是点![]() ;又过点
;又过点![]() 作曲线C的切线,切点为
作曲线C的切线,切点为![]() ,设
,设![]() 在x轴上的投影是
在x轴上的投影是![]() ;…;依此下去,得到一系列点
;…;依此下去,得到一系列点![]() ,
,![]() ,…,
,…,![]() ,…,设点
,…,设点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)试求数列{![]() }的通项公式
}的通项公式![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(Ⅱ)求证:![]()
(Ⅲ)求证:![]() (注:
(注:![]() ).
).
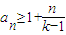 ;
; (注:
(注: ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com