本题满分14分)

已知函数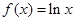,,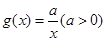设.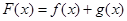

(Ⅰ)求函数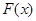的单调区间；

(Ⅱ)若以函数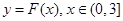图像上任意一点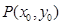为切点的切线的斜率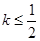恒成立,求实数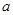的最小值；

(Ⅲ)是否存在实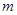数,使得函数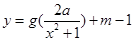的图像与函数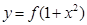的图像恰有四个不同的交点？若存在，求出实数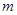的取值范围；若不存在,说明理由.

(本题满分14分)．有一块边长为4的正方形钢板，现对其切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计)．有人应用数学知识作如下设计：在钢板的四个角处各切去一个边长为的小正方形，剰余部分围成一个长方体，该长方体的高是小正方形的边长．

(1)请你求出这种切割、焊接而成的长方体容器的的容积V₁（用表示）；

(2)经过设计（1）的方法，计算得到当时，V_l取最大值，为了材料浪费最少，工人师傅还实践出了其它焊接方法，请写出与（1）的焊接方法更佳（使材料浪费最少，容积比V_l大）的设计方案，并计算利用你的设计方案所得到的容器的容积。

（本题14分）口袋内有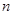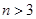（）个大小相同的球，其中有3个红球和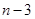个白球．已知从

口袋中随机取出一个球是红球的概率是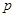，且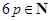。若有放回地从口袋中连续地取四次球（每次只取一个球），在四次取球中恰好取到两次红球的概率大于。

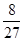（Ⅰ）求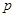和；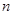

（Ⅱ）不放回地从口袋中取球（每次只取一个球），取到白球时即停止取球，记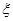为第一次取到白球时的取球次数，求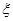的分布列和期望。

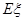（本题满分14分）

已知函数，，记

（Ⅰ）求的单调区间；

（Ⅱ）当时，若，比较：与的大小；

（Ⅲ）若的极值为，问是否存在实数，使方程

有四个不同实数根？若存在，求出实数的取值范围；若不存在，请说明理由。

（本题满分14分）

已知函数，，记

（Ⅰ）求的单调区间；

（Ⅱ）当时，若，比较：与的大小；

（Ⅲ）若的极值为，问是否存在实数，使方程

有四个不同实数根？若存在，求出实数的取值范围；若不存在，请说明理由。